

The precomputation phase is performed directly during the interaction, so that only
data needed for the approximation of the deformations for the actual and close positions
of the haptic interaction point (HIP) are calculated and immediately used for the interpolation.
There are two main advantages of this approach. First, as the deformations needed
for the interpolations are computed according to the actual position and motion of
HIP, construction of the entire state-space is not needed anymore. Further, any
parameter can be changed any time when no interaction between the HIP and the
body occurs.
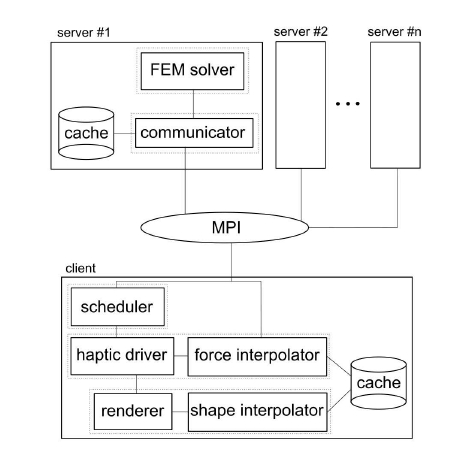
Scheme of the algorithm components (solid-outlined boxes) grouped in threads (dashed-outlined boxes) on local level and client and servers on global level.
The architecture of our application is based on single client multiple servers model. The client proces runs on computer where the haptic device and display is attached. The component named scheduler searches for nearest unknown states in cloud (states close to HIP) and schedules its solving on server processes. The server process solves states, sending them asynchnonously to client or another server processes if it is needed (the new state is computed from some alredy solved naighbour state which can be cached by other server). Finally, the client process interpolated the actual haptic force and tissue shape by interpolation of solved states.
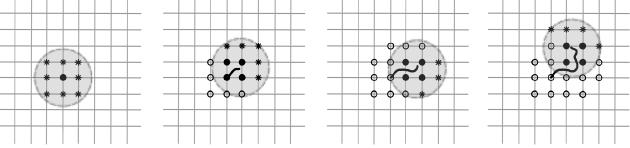
Four snapshots of the on-line precomputations. The trajectory of the HIP is visualized by thick black curve, the actual vicinity around the HIP is depicted by gray circle and states are denoted as follows: full circles show the states computed before and actually used for the interpolation, empty circles show the states computed before and currently unused (cached) and stars show states being actually computed to be potentially used after cell switching.
The model of human liver consists of 1 777 elements has been used in our
experiments. We have two material laws implemented; StVenant-Kirchhoff and
Mooney-Rivlin with incompresibility constraints.
First, the convergence of large deformations and speed of computation has been
measured. The convergence problems were identified by occurrence of failure points where
the convergence was not achieved anymore. The failure points can be therefore
regarded as “boundaries” determining the parts of state space where the deformations
can be safely computed for any position of HIP. The speed of particular states solving
limits the maximal linear speed of HIP, because each new state can be computed using
some alredy solved neighbour state (linear motion of HIP is worst case). In current
implementation, the linear speed of HIP is limited to 3.28 mm/s for Mooney-Rivlin
and 5.25 mm/s for StVenant-Kirchhoff.
| Material | StVenant | Mooney |
|---|---|---|
| Assembly time [s] | 0.21 | 0.51 |
| Solution time [s] | 0.03 | 0.11 |
| Line Search time [s] | 0.05 | 0.14 |
| Occurrence of failure points [%] | 19.7 | 1.4 |
| Average number of iters. | 2.4 | 4.2 |
| Maximal number of iters. | 10 | 14 |
The second measured parameter is maximal number of processor cores allocated by scheduler when the cloud moves maximal speed mentioned above. The computational resources need of our application is measured for multiple cloud sizes.
| Cloud size [cm] | 2.0 | 2.5 | 3.0 | 3.5 |
|---|---|---|---|---|
| #processes needed for StVenant | 15 | 31 | 37 | 57 |
| #processes needed for Mooney | 15 | 35 | 44 | 56 |